Statement Encoding

The GKR protocol specifically works with statements of the form $C(y)=0$, where $C$ is a layered arithmetic circuit. Define a singular value, $0$, to be the output layer, ${\mathcal{L}}_0$, and the input values $y_i$ to make up the input layer, ${\mathcal{L}}_d$.

For any layer, the following invariant holds: if a value is in ${\mathcal{L}}_i$, then it must be the result of a binary operation involving values in layers $j,k$ such that $j>i,k>i$. It is possible that $j=k$, but not necessary.

These binary operations are usually referred to as "gates." In the following tutorial we will be focusing on two gates: $\mathrm{add}$ gates, which are represented by the following function:

$$\mathrm{add}(z,x,y):\{0,1{\}}^{s_i+s_j+s_k}\mapsto \{0,1\}=\{\begin{array}{ll}1,& \text{if }{\mathrm{val}}_j(x)+{\mathrm{val}}_k(y)={\mathrm{val}}_i(z)\\ 0,& \text{otherwise}\end{array}$$ and $\mathrm{mul}$ gates: $$\mathrm{mul}(z,x,y):\{0,1{\}}^{s_i+s_j+s_k}\mapsto \{0,1\}=\{\begin{array}{ll}1,& \text{if }{\mathrm{val}}_j(x)\cdot {\mathrm{val}}_k(y)={\mathrm{val}}_i(z)\\ 0,& \text{otherwise}\end{array}$$

In other words, if we think of a physical representation of $C$, the binary gates represent the "wires" of the circuit. They show how the values from wires belonging in previous layers of the circuit can be used to compute a value in a future layer (from input to output). In fact, for every value with label $z$ in layer $i\ne 0:\exists x,y$ such that $\mathrm{add}(z,x,y)=1$ or $\mathrm{mul}(z,x,y)=1$ for $x,y$ as labels for values in layers $j,k>i$.

Example

Let's look at the following layered arithmetic circuit with depth $d$ = 3:

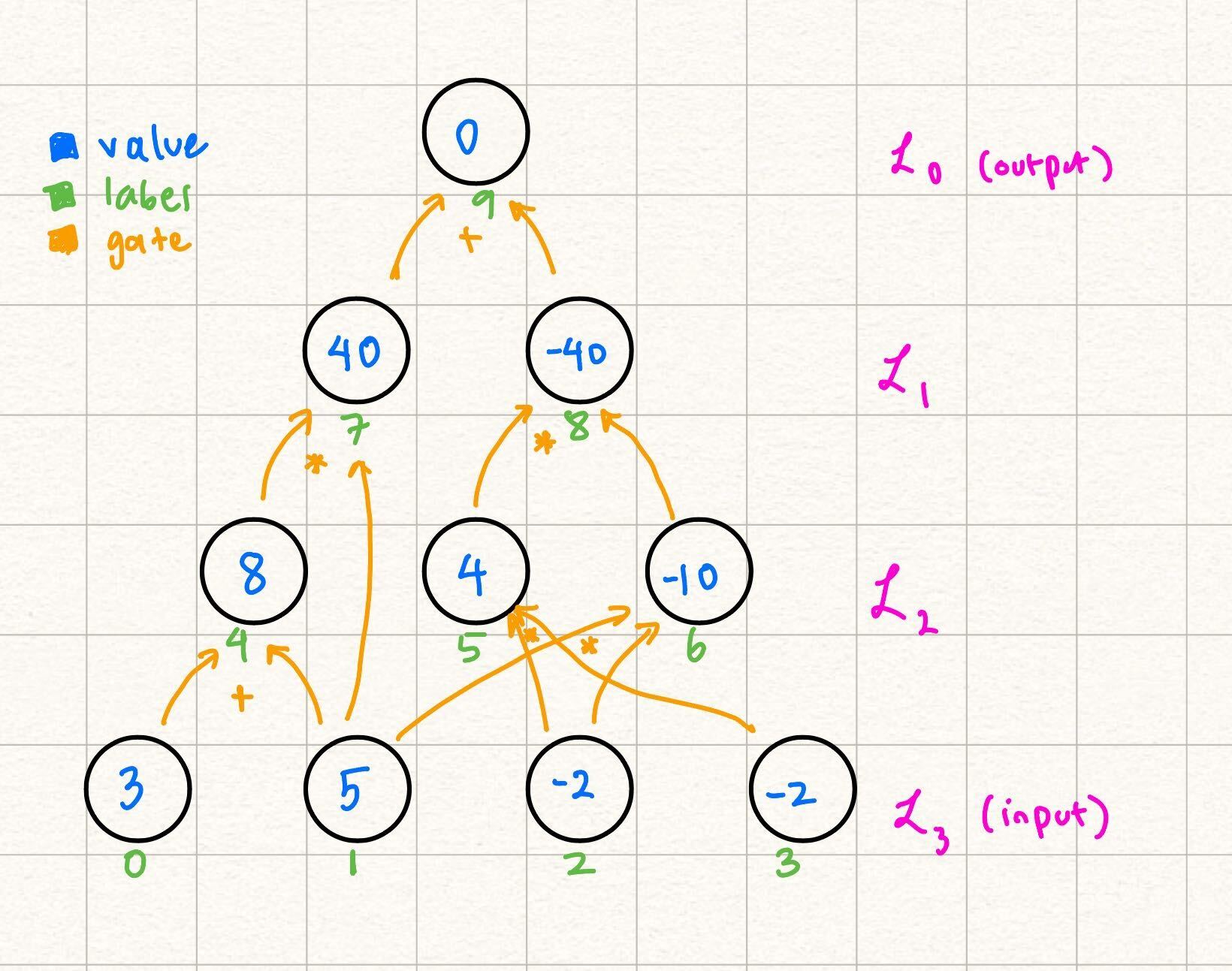
In this case, $\mathrm{add}(4,0,1)=1$ and $\mathrm{mul}(4,0,1)=0$, but $\mathrm{mul}(7,4,1)=1$. Notice how the circuit naturally falls in "layers" based on the dependencies of values.